Area of a Triangle Calculator

1. Area of a triangle
2. Area of a Triangle calculation
3. Rules for solving a triangle
4. Examples: find the area of a triangle
5. Practical application of triangle geometry

    Area of a triangle

The formula for the area of a triangle is side x height, as shown in the graph below:

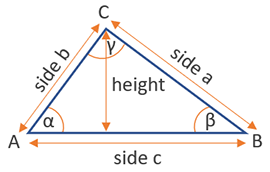
There are different starting measurements from which one can solve a triangle, calculate the length of a side and height to it, and finally calculate a triangle's area. There are 4 common rules for solving a triangle, as explained below.

    Area of a Triangle calculation

Aside from the basic formula of side x height, we have the SSS, ASA, SAS, and SSA rules for solving a triangle, where S is a side length and A is the angle in degrees. The abbreviations denote our starting measurements. Our area of triangle calculator supports the basic formula, these four rules, and the hypotenuse and the length of one of the other sides rule for right-angled triangles only.

    Rules for solving a triangle

So, how to calculate the area of a triangle using more advanced rules? You can solve the whole triangle starting from different sets of measurements:

• SSS (side-side-side) - you basically have all three sides, from which you can calculate the angles, and from there - the height, using the Pythagorean theorem.
• SAS (side-angle-side) - having the lengths of two sides and the included angle (the angle between the two), you can calculate the remaining angles and sides, then use the SSS rule.
• SSA (side-side-angle) - having the lengths of two sides and a non-included angle (an angle that is not between the two), you can solve the whole triangle.
• ASA (angle-side-angle) - having the measurements of two angles and the side which serves as an arm for both (is between them), you can fully solve the triangle.

Some of the above rules rely on the Law of Sines and the Law of Cosines, making it a requirement for you to understand them before you can apply these rules without the help of our area of a triangle calculator. The law of sines basically states that each side and its opposing angle's sine are related in the same way: The law of cosines is a generalization of the Pythagorean theorem and it tells us that c² = a² + b² - 2ab·cosγ using the side and angle notations from our calculator graph above.

Another rule, supported by our calculator is just for right-angled triangles: if you are given the length of the hypotenuse and one of the other sides, you can easily compute the third side using the Pythagorean theorem, and then use it again to get to one of the heights.

    Examples: find the area of a triangle

Example 1: Using the illustration above, take as given that b = 10 cm, c = 14 cm and α = 45°, and find the area of the triangle. In this case the SAS rule applies and the area can be calculated by solving (b x c x sinα) / 2 = (10 x 14 x sin(45)) / 2 = (140 x 0.707107) / 2 = 99 / 2 = 49.5 cm².

Example 2: If one side of the triangle is known to be 6 inches in length, and the height perpendicular to it is 4 inches in length, what is the triangle's area? This is a straightforward application of the side and height rule which calls for a simple multiplication of the two, and then a division by two. So (6 x 4) / 2 = 24 / 2 = 12 sq in.

Example 3: Find the area of a triangle-shaped garden given one side of it (say, c) is 15 feet long and the two adjacent angles are 30° and 60°. This task can be resolved using the ASA rule. Solving using the area of a triangle formula c² / (2 * (tanα^-1 + tanβ^-1)) = 225 / (2 * (0.577350^-1 + 1.732051^-1)) = 48.7 square feet. Obviously using both a tangent calculator and an exponent calculator is quite helpful.

    Practical application of triangle geometry

An everyday use of triangle math is if you want to lay tiles at perfect 90° or 45° to the sides of a room. The reference lines are established using the 3-4-5 rule. If you want to know how long a ladder should be so it can reach a given height at a given angle with the ground. Steel and wooden structures like houses, bridges, warehouses, etc. often use triangular support.

More advanced applications are crucial to surveying and GPS (triangulation). Mobile network operators can establish your location by triangulating your signal using 3 or more base towers which are in range. Flight paths of planes also require triangle calculations.