Acceleration Calculator
Easily calculate the acceleration, starting and final speed, or time to reach a given speed with this acceleration calculator. Supported metrics are meters per second, miles per hour, miles per second, km per hour, km per second, yards/feet per second and knots. Output is in meters per second squared and standard gravity (g, g-units).
About the acceleration calculator
This acceleration calculator is useful for any kind of vehicle or object: car, bus, train, bike, motorcycle, plane, ship, space craft, projectile, etc. due to the many different units supported. You need to know 3 of the 4: acceleration, initial speed, final speed and time (acceleration duration) to calculate the fourth.
The output is always in the input unit squared (e.g. km/h2), meters per second squared (m/s2) and standard gravity units (gn, often just g).
The calculator can be used to calculate deceleration as well, simply by entering a lower value for the final speed. It can be used to estimate the deceleration required to come to a full stop in a given number of seconds, for example, or the breaking path of a vehicle decelerating at a given rate.
Standard Gravity
gn is equal to 9.80665 m/s2 and is the standard acceleration due to Earth's gravity according to the International Service of Weights and Measures [1][2]. The value of ɡn is a nominal midrange value on Earth, originally based on the acceleration of a body in free fall at sea level at a geodetic latitude of 45°, the actual acceleration of free fall on Earth varies according to location.
The human body can handle a different amount of g-force depending on whether it is perpendicular to or along the spine. If perpendicular, many humans can endure 20g for about 10 seconds, 10g for a minute, and 6g for up to 10 minutes, without any ill effects. However, the human body deals much worse with vertical g-forces that are aligned with the spine. A typical person can handle 5g for a short duration without passing out, while trained pilots with suits and other equipment can withstand 9g for prolonged periods of time. Negative g-force is much harder to handle, with the limit being between -2g and -3g.
Acceleration formula
The formula for acceleration expressed in terms of the initial velocity (speed), final velocity and the acceleration duration (time) is:
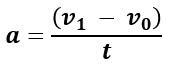
where a is the acceleration, v0 is the starting velocity, v1 is the final velocity, and t is the time (acceleration duration or t1 - t0). The resulting unit will depend on the units for both time and distance, so if your input was in miles and hours, the acceleration will be in miles/h2. If it was in meters and seconds, it would be in m/s2 (meters per second squared). Remember to always have the time unit of the speed measure being the same as the duration measure.
Equations for initial velocity, final velocity, and time
Variants of the formula above are used when solving for initial velocity, final velocity or time. The equation is to be rearranged in the following way depending on what is to be found:
- to find the initial velocity (v0): v1 - a / t
- to find the final velocity (v1): v0 + a / t
- to find the time (t): (v1 - v0) / a
Initial velocity is often incorrectly referred to as initial speed, but the correct term is usually velocity since it represents the magnitude of a vector and therefore has direction. Speed, on the other hand, is a scalar value and does not indicate direction. The acceleration solver above will apply the correct formula depending on what it has to solve for.
Calculation examples
Example 1: A car starts at 0 mph and accelerates to 60 miles per hour in 8 seconds. What is its average acceleration during these eight seconds? The answer is (60 mph - 0 mph) / 8s = (26.8224 m/s - 0 m/s) / 8s = 3.3528 m/s2 (meters per second squared) average car acceleration. That would be 27,000 miles per hour squared.

Example 2: A truck is travelling at 50 km/h and increases its velocity to 65 km per hour in 10 seconds. Find its average acceleration? The answer is (65 kmph - 50 kmph) / 10s = (18.055 m/s - 13.888888 m/s) / 10s = 0.416667 m/s2 (meters per second squared).
Example 3: If a ship is moving at 20 knots and you want to know how hard you should decelerate in order to reach a full stop in 30 seconds, you need to calculate (0 knots - 20 knots) / 30s = -33.76 ft/s / 30s = -1.1252 ft/s2 or -0.342963 m/s2.
Example 4: A plane takes off at a certain speed and then accelerates for 2 minutes by 1.6 m/s2 on average to reach cruising altitude and velocity which is 900 km/h. What is the initial speed / initial velocity of the plane? To calculate this, use the first variant of the acceleration formula and replace the known variables: 900 km/h - 1.6 m/s2 · 2 min. After the necessary unit conversion we arrive at the solution: 250 m/s - 1.6 m/s2 · 120 s = 250 m/s - 192 m/s = 58 m/s or ~209 km/h.
References
1 NIST Special Publication 330 (2008) - "The International System of Units (SI)", edited by Barry N.Taylor and Ambler Thompson, p. 52
2 "The International System of Units" (SI) (2006, 8th ed.). Bureau international des poids et mesures pp. 142–143. ISBN 92-822-2213-6
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Acceleration Calculator", [online] Available at: https://www.gigacalculator.com/calculators/acceleration-calculator.php URL [Accessed Date: 31 Dec, 2025].