Ideal Gas Law Calculator
Easily calculate the pressure, volume, temperature or quantity in moles of a gas using this combined gas law calculator (Boyle's law calculator, Charles's law calculator, Avogadro's law calculator and Gay Lussac's law calculator in one). Supports a variety of input metrics such as Celsius, Fahrenheit, Kelvin, Pascals, bars, atmospheres, and volume in both metric and imperial units cubed. Also known as a PV = nRT calculator due to the ideal gas formula.
- About the gas laws calculator
- Gas law formulas
- Ideal Gas Law Formula
- Boyle's Law Formula
- Charles's Law Formula
- Gay-Lussac's Law Formula
- Avogadro's Law Formula
- Combined Gas Law Formula
- Applicability of the ideal gas formula
About the gas laws calculator
This is an ideal gas law calculator which incorporates the Boyle's law , Charles's law, Avogadro's law and Gay Lussac's law into one easy to use tool you can use as a:
- gas pressure calculator
- gas volume calculator
- gas quantity calculator
- gas temperature calculator
Simply enter the three known measures to calculate the fourth. The calculator uses the combined gas law formula discussed below to perform the computations. It supports both imperial and metric units for volume and pressure and 5 different temperature scales: Kelvin, Celsius, Fahrenheit, Rankine and Reamur, both as input and as output.
The units supported for volume are: mm3, cm3, m3, ml, L (litre), gallons, fluid ounces, cubic inches, cubic feet and cubic yards. Units supported for pressure are Pascals, kiloPascals, MegaPascals, GigaPascals, millibars, bars, atmospheres, millimeters of Hg liquid, millimeters of H2O liquid, and pound-force per square inches (psi).
Gas law formulas
The gas law calculator uses a combination of several formulas for the behavior of gases which can be derived from four separate gas law formulas and result in the ideal gas formula shown below.
Ideal Gas Law Formula
The ideal gas law is the equation for the state of a hypothetical ideal gas.
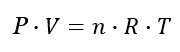
where P is the pressure in Pascals, V is the volume in m3, n is the quantity in moles, T is the absolute temperature in Kelvins and finally R is the universal gas constant. R is equivalent to the Boltzmann constant, but expressed in units of energy per temperature increment per mole (the pressure–volume product). In SI based units it is 8.3144598(48) kg⋅m2⋅mol−1⋅K−1⋅s−2. Due to this formula people would often refer to the above tool as a "PV nRT calculator". A mole is the amount of substance which contains as many elementary entities as there are atoms in 12 g of carbon-12.
Another way to express the right side of the equation is N · kb · T: the number of gas molecules times the Boltzman constant times the absolute temperature.
The ideal gas formula was first stated by the French engineer and physicist Emile Clapeyron in 1834 based on four component formulas, discussed below.
Boyle's Law Formula
With Boyle's law we have that for a constant temperature and gas quantity the pressure of a gas multiplied by its volume is also constant:

This means that under the same temperature, two gases with equal quantity of molecules and equal volume must also have the same pressure, as well as that two gases with equal quantity and pressure must have the same volume.
Charles's Law Formula
With Charles' law we have that for a constant pressure and gas quantity its volume divided by its temperature is constant:

Gay-Lussac's Law Formula
With Gay-Lussac's law we have that for a constant volume and gas quantity the pressure of a gas divided by its temperature is a constant:

Avogadro's Law Formula
Avogadro's law states that if we have constant temperature and pressure the gas volume divided by the gas quantity is a constant. Under these conditions, if two gases have the same volume, they must necessarily contain the same molecular quantities.

Combined Gas Law Formula
The combined gas law formula states that with a constant quantity of gas the gas pressure multiplied by its volume and divided by its temperature is also constant:

The appropriate formula from the ones listed above is chosen automatically when you use this ideal gas law calculator.
Applicability of the ideal gas formula
Understanding when the ideal gas formula applies and when it does not is a key prerequisite in making sure you use this ideal gas law calculator accordingly. The equation for the ideal gas (PV=nRT) applies only to, well, an ideal gas. If a real gas behaves sufficiently like an ideal gas the formula can be used as an approximation depending on the required margin of error.
The major issue with the idea gas law is that it neglects both molecular size and intermolecular attractions, therefore it is most accurate for monatomic gases at high temperatures and low pressures. With lower densities (large volume at low pressure) the neglect of molecular size becomes less critical since the average distance between adjacent molecules becomes much larger relative to the size of the molecules themselves. Increasing temperature means higher thermal kinetic energy which diminishes the relative importance of intermolecular attractions.
For a more precise equation of state you might want to use the van der Waals equation calculator instead of the ideal gas law calculator above.
References
1 NIST Special Publication 330 (2008) - "The International System of Units (SI)", edited by Barry N.Taylor and Ambler Thompson, p. 52
2 "The International System of Units" (SI) (2006, 8th ed.). Bureau international des poids et mesures pp. 142–143. ISBN 92-822-2213-6
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Ideal Gas Law Calculator", [online] Available at: https://www.gigacalculator.com/calculators/ideal-gas-law-calculator.php URL [Accessed Date: 10 Jan, 2026].