Angular Velocity Calculator
Easily calculate the angular velocity of an object in circular motion. Input supports metric and imperial measurement units, radians and degrees. The angular speed calculator can also be used to solve for linear velocity and radius. Can also convert angular speed to linear speed and vice versa.
Using the angular velocity calculator
Angular velocity of an object or particle is the rate at which it rotates around a chosen center point or in other words: what angular distance does an object cover around something over a period of time and is measured in angle per unit time. The standard measurement is in radians per second, although degrees per second, revolutions per minute (rpm) and other units are frequently used in practice and our calculator supports most of them as an output unit.
This angular speed calculator is useful for estimating the angular velocity of a body in motion on a circular path. For example, it can be used to calculate the angular speed of a Ferris wheel, a carousel, a CD-ROM or DVD, and basically any object which is rotating or moving on a circular path. It even works well enough for calculating the angular momentum at the Earth's surface and angular speed in its orbit around the Sun (see example #3 below), even though these are not exact circles. If RPM is known it can serve as an RPM to angular velocity calculator.
This online tool can be used to calculate angular velocity based on known angle turn distance and time (angular distance covered and time to cover it) as well as based on linear speed and the radius of the circular path the object or particle is on. The tool can also be used to solve for linear velocity or radius given the angular velocity and the other of the two, thus functioning as both a linear velocity to angular velocity and an angular velocity to linear velocity converter (linear velocity calculator).
The output if calculating linear velocity is in both metric and imperial units: m/s, ft/s, km/s, km/h, miles/s and mph. When the output is the path radius is given in meters, feet, kilometers, miles and even light years and parsecs for really large distances.
Angular Velocity Equations
The angular velocity vector always runs perpendicular to the plane in which the object is rotating which makes the equations for finding it quite simple. The formula for angular velocity (ω, Greek lower-case letter omega) in radians expressed in terms of the body's rotation frequency (f) is the first equation below:
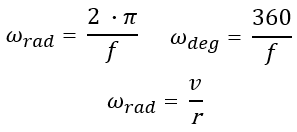
whereas the second equation represents the angular velocity in radians. The third formula is for angular velocity when we know the object's linear velocity and the radius of the circular path. Through a simple transformation of the third equation we get the linear velocity formula:

These formulae are valid for rigid bodies and work for non-rigid ones only approximately.
Angular Speed Calculation Examples
Example 1: A kid's carousel is rotating with 10 revolutions per minute. What is its angular velocity in degrees per second? First, convert revolutions per minute to degrees per minute. Since one revolution is 360°, 10 revolutions would be 3600° per minute. A minute has 60 seconds, so we simply divide 3600 by 60 to get 60°/s. This calculation can also be performed by utilizing the first and second angular speed equation above: f = 60/10 = 6 seconds per rotation so ωdeg = 360 / 6 = 60°/sec and ωrad = 2 · π / 60°/s = 6.283184 / 6 = 1.0471973 radians per second.
Example 2: A Ferris wheel with a radius of 20 meters is spinning to produce a linear velocity of 0.5 m/s. What is the angular velocity of the Ferris wheel in radians per second? We simply use the formula ωrad = r / v = 20 / 0.5 = 0.0250 radians per second. Using the tool above in linear speed calculator mode will confirm the math.

Example 3: Find the distance from the Earth to the Sun if you know that the Orbital speed of the Earth is 29,800 m/s and, of course, that it makes one revolution around the Sun in 1 year. First, we need to convert revolutions per year to radians per second by multiplying 1 year to 2 · π = 6.283184 and then we need to divide by (86,400 sec * 365.2421 days) to get 0.000000199106434243010 radians per second. The solution is then simple by using the formula r = v / ω = 29,800 m/s / 0.000000199106434243010 = 149668694099.701 meters or about 149,667 km (~93,000 miles) - which is exactly the estimated distance between the Earth and the Sun (check calculation).
Of course, while using our calculator you would not need to perform these unit conversions, as they are handled for you on the fly.
References
1 NIST Special Publication 330 (2008) - "The International System of Units (SI)", edited by Barry N.Taylor and Ambler Thompson, p. 52
2 "The International System of Units" (SI) (2006, 8th ed.). Bureau international des poids et mesures pp. 142–143. ISBN 92-822-2213-6
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Angular Velocity Calculator", [online] Available at: https://www.gigacalculator.com/calculators/angular-speed-calculator.php URL [Accessed Date: 03 Jan, 2026].