Chi-Square Calculator
Use this Chi Square calculator to easily test contingency tables of categorical variables for independence or for a goodness-of-fit test. Can be used as a Chi-Square goodness-of-fit calculator, as a Chi-Square test of independence calculator or as a test of homogeneity. Supports unlimited numbers of rows and columns (groups and categories): 2x2, 3x3, 4x4, 5x5, 2x3, 2x4 and arbitrary N x M contingency tables. Outputs Χ2 and p-value.
- Using the Chi-Square calculator
- What is a "Chi Squared test"?
- Chi-Square Formula
- Types of Chi-Square tests
Using the Chi-Square calculator
The above easy to use tool can function in two main modes: as a goodness-of-fit test and as a test of independence / homogeneity. These modes apply to different situations covered in detail below. The mode of operation can be selected from the radio button below the data input field in the Chi Square calculator interface.
As a Chi-Square Test of Independence or Homogeneity
Copy/paste the data from a spreadsheet file into the data input field of the calculator or input it manually by using space ( ) as a column separator and new line as a row separator. The data in all cells should be entered as counts (whole numbers, integers). For example, if you have this data in Excel:
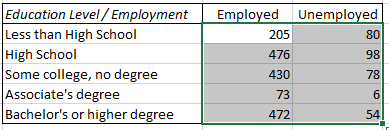
simply copy and paste the numerical cells into the calculator's input field above. Click here to see how this example works. If the sample data is known to be independent the result can be treated as a test of homogeneity. If the data is based on two categorical variables measured from the same population the result can be interpreted as a test of independence between the variables.
As a Chi-Square Test of Goodness-of-Fit
The chi-square test calculator can be used as a goodness-of-fit calculator by entering the observed values (counts) in the first column and the expected frequencies for each outcome in the second column. The expected frequencies should sum up to ~1. For example, if we are testing if a dice is fair, we would have an expected frequency of 0.1666(6) for each number. An example data set might look like so:
| Number | Times turned up | Expected Frequency |
|---|---|---|
| 1 | 168 | 0.1666 |
| 2 | 170 | 0.1666 |
| 3 | 160 | 0.1666 |
| 4 | 163 | 0.1666 |
| 5 | 173 | 0.1666 |
| 6 | 166 | 0.1666 |
| Sum total | 1000 | 1 |
Make sure to select the appropriate type of test "Chi-Square test of Goodness-of-fit".
What is a "Chi Squared test"?
A Chi-Squared test is any statistical test in which the sampling distribution of the parameter is Χ2-distributed under the null hypothesis and thus refers to a whole host of different kinds of tests that rely on this distribution. In its original version it was developed by Karl Pearson in 1900 as a goodness of fit test: testing whether a particular set of observed data fits a frequency distribution from the Pearson family of distributions (Pearson's Chi-Squared test). Pearson in 1904 expanded its application to a test of independence between the rows and columns of a contingency table of categorical variables [1]. It was further expanded by R. Fisher in 1922-24.
The statistical model behind the tests requires that the variables are the result of simple random sampling and are thus independent and identically distributed (ID) (under the null hypothesis). Consequently, the test can be used as a test for independence or a test for homogeneity (identity of distributions). In certain restricted situations it can also function as a test for the difference in variances. This, however, also means that if one wants to test non-IID data a different test should be chosen.
As with most statistical tests it performs poorly with very low sample size, in particular: because the Χ2 assumption might not hold well for the data at hand. For a simple 2 by 2 contingency table the requirement is that each cell has a value larger than 5. For larger tables no more than 20% of all cells should have values under 5. Our chi-square calculator will check for some of these conditions and issue warnings where appropriate.
Chi-Square Formula
The formula is the same regardless if you are doing a test of goodness-of-fit, test of independence or of homogeneity. Despite the formula behind all three tests being the same, however, all three have different null hypotheses and interpretations (see below). The Chi-Square formula is simply:
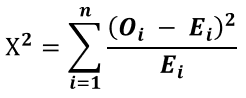
where n is the number of cells in the table and Oi and Ei are the observed and expected values of each cell. The resulting Χ2 statistic's cumulative distribution function is calculated from a chi-square distribution with (r - 1) · (c - 1) degrees of freedom (r - number of rows, c - number of columns).
Types of Chi-Square tests
Here we examine the three applications of the Chi Square test: as a test of independence, as a test of homogeneity (identical distribution) and as a goodness-of-fit test.
Chi-Square Test of Independence
This test is also sometimes referred to as a "test of association" and it determines whether two categorical variables for a single sample are independent or associated with each other. For example, a survey might ask respondents to state their education level, height and net wealth in order to determine whether there is some dependence on one variable on the others. The null hypothesis H0 would thus be: the variables education, height and wealth are independent. The alternative hypothesis H1 is then: "some of the variables education, height and net wealth are dependent on each other". Note that in case there are more than two variables the null will be rejected even if some variables are independent of each other: one dependence in a table is enough to potentially invalidate the null.
When using the calculator as a test for independence obtaining a small p-value is to be interpreted as evidence that the two (or more) groups are not independent. Note that if there are more than two variables you cannot say which ones are independent and which are not: it might be all of them or just some of them.
Chi-Square Test of Homogeneity
This test refers to testing if two or more variables share the same probability distribution and is also supported by this online Chi Square calculator. The test of homogeneity is used to determine whether two or more independent samples differ in their distributions on a single variable of interest: comparing two or more groups on a categorical outcome. For example, one can compare the educational levels of groups of people from different cities in a country to determine if the proportions between the groups are essentially the same or if there is a statistically significant difference. The null hypothesis H0 is that the proportions between the groups are the same while the alternative H1 is that they are different.
Note that upon observing a low p-value one can only say that at least one proportion is different from at least one other proportion, but we cannot say which. Further procedures such as Sheffe, Holm or Dunn-Bonferroni need to be deployed to select a suitable critical value for the further tests to identify pairwise significant differences.
When technically feasible, randomization is often used to produce independent samples.
Chi-Square Goodness-of-Fit Test
The goodness-of-fit test can be used to assess how well a certain frequency distribution matches an expected (or known) distribution. The null hypothesis H0 is that the data follows a specified distribution while the alternative H1 is that it does not follow that distribution. Rejecting the null means the sample differs from the population on the variable of interest.
For example, if we know that a fair dice should produce each number with a frequency of 1/6 then we can roll a dice 1,000 times, record how many times we observed a given number and then check it against the ideal dice distribution to see if it is fair. If the observations we get are 168 ones, 170 twos, 160 threes, 163 fours, 173 fives and 166 sixes, do we have evidence the dice is rigged? Load example data in the calculator to perform the calculation.
Another example is in population surveys where a representative survey across a certain demographic dimension or geographic locale is required. Knowing the age distribution of the whole population from a recent census or birth & death registries, you can compare the frequencies in your sample to those of the entire population. With a big enough sample the test will be sensitive enough to pick any substantial discrepancy between your sample and the population you are trying to represent.
Yet another application is found in online A/B testing where a Chi-Square goodness-of-fit test is the statistical basis for performing an SRM check. It is used to detect various departures from the assumed statistical model such as randomizer bias, issues with experiment triggering, tracking, log processing, and so on.
Comparing the three types of Chi-Square tests
This table offers a quick reference to the differences between the three main uses of the Χ2 test and should be useful to anyone using our X2 calculator for any purpose.
| Attribute | Test of Independence | Test of Homogeneity | Test of Goodness of Fit |
|---|---|---|---|
| Sampling type | Single depenendent sample | 2 or more independent samples | Sample from a population |
| Null hypothesis | The variables are independent | The proportions between groups are the same | The sample's distribution is the same as the population distribution |
| Null rejected | Infer the variables are dependent | Infer the proportions are different | Infer the sample's distribution is different than that of the population |
Other tests
Under certain conditions the X2 test can be used as a test for the difference in variances. When both marginal distributions are fixed the Chi-Square test can also be used as a test of unrelated classification.
References
1 Franke T.M. (2012) – "The Chi-Square Test: Often Used and More Often Misinterpreted", American Journal of Evaluation, 33:448 DOI: 10.1177/1098214011426594
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Chi-Square Calculator", [online] Available at: https://www.gigacalculator.com/calculators/chi-square-calculator.php URL [Accessed Date: 09 Jan, 2026].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:












 Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".
Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".