Normal Distribution Calculator
Use this calculator to easily calculate the p-value corresponding to the area under a normal curve below or above a given raw score or Z score, or the area between or outside two standard scores. With mean zero and standard deviation of one it functions as a standard normal distribution calculator (a.k.a. z table calculator), but you can enter any mean and standard deviation (sd, sigma). Alternatively, compute the Z score corresponding to a given probability or quantiles of any normal distribution by its inverse distribution function (IDF).
- How to use the normal distribution calculator
- What is a normal distribution
- Normal distribution formula
- Probability density function (PDF)
- Standard normal distribution function
- Cumulative distribution function (CDF)
- Inverse distribution function (quantile function, IDF)
- Why is the standard normal distribution useful?
How to use the normal distribution calculator
This calculator has three modes of operation: as a normal CDF calculator, as a probability to Z score calculator, and as an inverse normal distribution calculator. The first is useful in calculating the probability corresponding to the area under a normal curve below or above a given normal score (raw score). For example, one may want to compute a p-value as part of a test of statistical significance. It can also be used to determine the significance threshold corresponding to a given critical region specified by one or two standard scores.
The calculations in this mode are carried out using the cumulative distribution function of the normal distribution with the specified mean μ (mu) and standard deviation σ (sigma). The output also includes the computed Z score. With μ = 0 and σ = 1 the tool serves as a standard normal distribution calculator and the raw score entered is equal to a Z score.
In the second mode the inverse CDF of the standard normal distribution is used to compute a standardized score (Z score) corresponding to the selected level of statistical significance, a.k.a. α (alpha) threshold. The calculator outputs a single z-score for the one-tailed scenario (use with a minus in front to change tails, if necessary) and the two z scores defining the upper and lower critical regions for a two-tailed test of significance. These can be used in the odd case where one is appropriate.
In quantile mode computes the inverse distribution function (IDF) of any normal distribution given its mean, standard deviation, and a specific proportion (a.k.a. quantile). For example, to calculate the cut-off of the lower quartile (lower 25%) of a normal distribution simply enter 0.25. Likewise, enter 0.90 for the upper decile (upper 10%) cut-off.
The precision setting determines how many numbers after the decimal point the output is to be rounded to. High accuracy output of up to 25 significant digits is supported.
What is a normal distribution
The normal distribution is a continuous probability distribution for a real-valued random variable (X). It is symmetrical around the mean and its mean is also its median and mode. Due to its shape, it is sometimes referred to as "the Bell Curve", but there are other distributions which result in bell-shaped curves, so this may be misleading. It is also called a Gaussian distribution, Gauss, or Gauss-Laplace distribution, after famous mathematicians Gauss and Laplace who were instrumental in its description and popularization [1,2,3]. The probability density function of the normal distribution results in a graph like the one shown below.
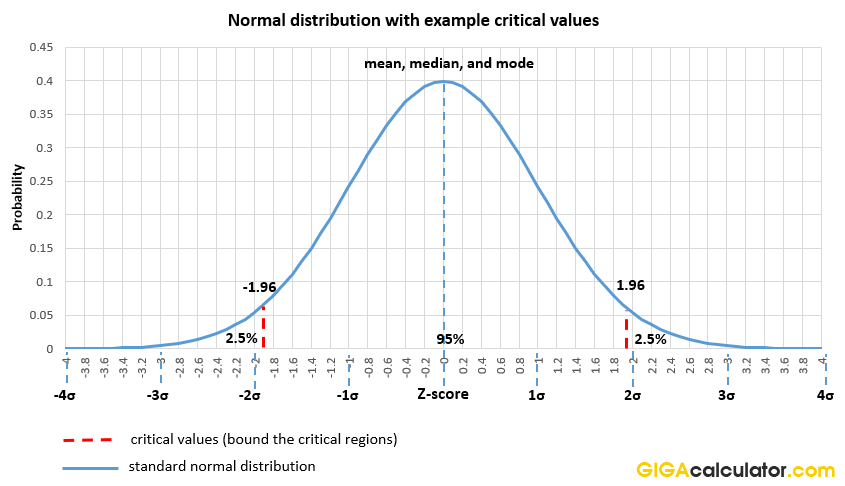
The normal distribution is non-zero over the entire real line, but values beyond ±4 sigma would appear to be zero on even high-resolution graphs which is why they are rarely plotted.
A very convenient feature of the normal distribution is that it can be fully described using only its first two moments (and hence also the first two cumulants) - the mean (μ) and the variance (σ2). All other moments have a value of zero. Since the standard deviation (σ, sigma) of a distribution is simply the square root of its variance and since standard deviation is a more convenient statistic compared to the variance, it is common to describe a normal distribution by its mean and standard deviation. Changing the mean of a distribution would shift it to the left or right.
The standard normal distribution, shown in the graph above, has a mean of 0 and a variance of 1. Its standard deviation is therefore 1 as well. The area under the standard normal curve sums up to one, hence the sum total of the probability is one. Increasing the standard deviation will result in a normal distribution in which the density is spread further away from the middle point, flattening the shape of the distribution. Decreasing it will make it more concentrated around the middle. Our calculator supports normal distributions with any real-valued mean and variance.
In statistical inference and statistical estimation, if a random variable has normally distributed error, critical regions can be defined based on probability values which are considered low enough to reject a given hypothesis as practiced in Null Hypothesis Statistical Testing (NHST). The idea is that if a given observation is rare enough under a specified null hypothesis model, it can serve as evidence against that model and by proxy - hypothesis [4]. The graph above shows two critical values at -1.96σ and 1.96σ. The area cut out by them on both sides of the distribution sums up to 5% cumulative probability. If one takes the area cut out just above the 1.96 z score then its cumulative probability is 2.5%. You can explore these cumulative probabilities using our Z distribution calculator (example).
Normal distribution formula
There are three key equations useful in dealing with normally distributed random variables - the probability density function (PDF) of the normal distribution, the cumulative distribution function (CDF), and its inverse (IDF). The first is useful in arriving at the second, which in turn is used when computing a p-value from a z-score. The third one is required when computing the z-score from a probability value.
Probability density function (PDF)
The formula for the probability density function of a general normal distribution with mean μ and variance σ2 is given by the equation:
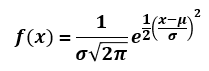
which is what is referred to as a "normal distribution formula". The density function is used to spread the probability across all possible values covered by the distribution (from plus to minus infinity). The density function can be viewed as representing the rate of change of the normal CDF shown below.
Standard normal distribution function
In the case of the standard normal distribution with a mean of zero and standard deviation of one these terms can simply be dropped from the above equation, simplifying it to:

which is sometimes referred to as the standard normal distribution formula.
Cumulative distribution function (CDF)
The cumulative probability density function, or cumulative distribution function for short (CDF) of the normal distribution takes the form of the integral equation:

where μ is the mean and σ is the standard deviation, and x is the z score of interest. This function is usually denoted with the capital Greek letter Φ (Phi).
Inverse distribution function (quantile function, IDF)
The inverse cumulative distribution function (a.k.a. ICDF, norm IDF, invnorm, or norminv) of the normal distribution is the inverse of the CDF and is given by the equation:

where erf-1 is the inverse error function, μ is the mean and σ is the standard deviation. The computation of normal quantiles is not straightforward which is why p value to z score tables were precomputed and distributed in the past. Nowadays a normal distribution probability calculator will easily compute the inverse function values for you. Simply select "Quantiles" in the interface and enter the required inputs.
Why is the standard normal distribution useful?
The standard normal distribution (μ = 0, σ = 1) sees a lot of use in the sciences and in statistical analyses performed as part of business experiments or observational analyses. Its utility is in providing standardized scores through which statistical discrepancies can be described in a unified and easy to communicate way. Two standard deviations away from the null means two standard deviations away regardless if one is measuring atomic mass displacement, the efficiency of a medical treatment, or changes in user behavior on an e-commerce website.
Standard scores, also called Z scores, correspond to certain quantiles of the standard normal distribution. These are shown below for whole z score values, but these quantiles are known for any z score value. Getting a Z score from a desired p-value threshold is also fairly straightforward with the use of an inverse normal distribution calculator like ours.

When conducting statistical analyses it is important to never take it for granted that your data has normally distributed errors, or is normally distributed itself. A test of normality should be performed to check if the normality assumption holds while noting that a high p-value from such a test does not necessarily mean normality can be assumed, especially with low numbers of observations. Some interesting and widely used statistics such as the difference of means of two distributions of any shape are known to be normally distributed thanks to the Central Limit Theorem (CLT). This makes the normal distribution applicable in multitudes of scenarios where a comparison between the means of distributions is of interest.
References
1 Gauss, C.F. (1809) "Theoria motvs corporvm coelestivm in sectionibvs conicis Solem ambientivm" [Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections]
2 Laplace, P-S (1774). "Mémoire sur la probabilité des causes par les événements". Mémoires de l'Académie Royale des Sciences de Paris (Savants étrangers), Tome 6: 621–656. Translated by Stephen M. Stigler in Statistical Science 1(3), 1986.
3 Laplace, P-S (1812). "Théorie analytique des probabilités" [Analytical theory of probabilities]
4 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science. The Netherlands: Elsevier.
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Normal Distribution Calculator", [online] Available at: https://www.gigacalculator.com/calculators/normal-distribution-calculator.php URL [Accessed Date: 02 Jan, 2026].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:












 Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".
Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".