Critical Value Calculator
Use this calculator for critical values to easily convert a significance level to its corresponding Z value, T score, F-score, or Chi-square value. Outputs the critical region as well. The tool supports one-tailed and two-tailed significance tests / probability values.
- Using the critical value calculator
- What is a critical value?
- T critical value calculation
- Z critical value calculation
- F critical value calculation
Using the critical value calculator
If you want to perform a statistical test of significance (a.k.a. significance test, statistical significance test), determining the value of the test statistic corresponding to the desired significance level is necessary. You need to know the desired error probability (p-value threshold, common values are 0.05, 0.01, 0.001) corresponding to the significance level of the test. If you know the significance level in percentages, simply subtract it from 100%. For example, 95% significance results in a probability of 100%-95% = 5% = 0.05.
Then you need to know the shape of the error distribution of the statistic of interest (not to be mistaken with the distribution of the underlying data!). Our critical value calculator supports statistics which are either:
- Z-distributed (normally distributed, e.g. absolute difference of means)
- T-distributed (Student's T distribution, usually appropriate for small sample sizes, equivalent to the normal for sample sizes over 30)
- X2-distributed (Chi square distribution, often used in goodness-of-fit tests, but also for tests of homogeneity or independence)
- F-distributed (Fisher-Snedecor distribution), usually used in analysis of variance (ANOVA)
Then, for distributions other than the normal one (Z), you need to know the degrees of freedom. For the F statistic there are two separate degrees of freedom - one for the numerator and one for the denominator.
Finally, to determine a critical region, one needs to know whether they are testing a point null versus a composite alternative (on both sides) or a composite null versus (covering one side of the distribution) a composite alternative (covering the other). Basically, it comes down to whether the inference is going to contain claims regarding the direction of the effect or not. Should one want to claim anything about the direction of the effect, the corresponding null hypothesis is direction as well (one-sided hypothesis).
Depending on the type of test - one-tailed or two-tailed, the calculator will output the critical value or values and the corresponding critical region. For one-sided tests it will output both possible regions, whereas for a two-sided test it will output the union of the two critical regions on the opposite sides of the distribution.
What is a critical value?
A critical value (or values) is a point on the support of an error distribution which bounds a critical region from above or below. If the statistics falls below or above a critical value (depending on the type of hypothesis, but it has to fall inside the critical region) then a test is declared statistically significant at the corresponding significance level. For example, in a two-tailed Z test with critical values -1.96 and 1.96 (corresponding to 0.05 significance level) the critical regions are from -∞ to -1.96 and from 1.96 to +∞. Therefore, if the statistic falls below -1.96 or above 1.96, the null hypothesis test is statistically significant.
You can think of the critical value as a cutoff point beyond which events are considered rare enough to count as evidence against the specified null hypothesis. It is a value achieved by a distance function with probability equal to or greater than the significance level under the specified null hypothesis. In an error-probabilistic framework, a proper distance function based on a test statistic takes the generic form [1]:
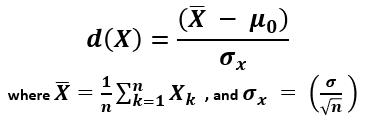
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ0 is the observed mean / treatment group mean, while σx is the standard error of the mean (SEM, or standard deviation of the error of the mean).
Here is how it looks in practice when the error is normally distributed (Z distribution) with a one-tailed null and alternative hypotheses and a significance level α set to 0.05:

And here is the same significance level when applied to a point null and a two-tailed alternative hypothesis:
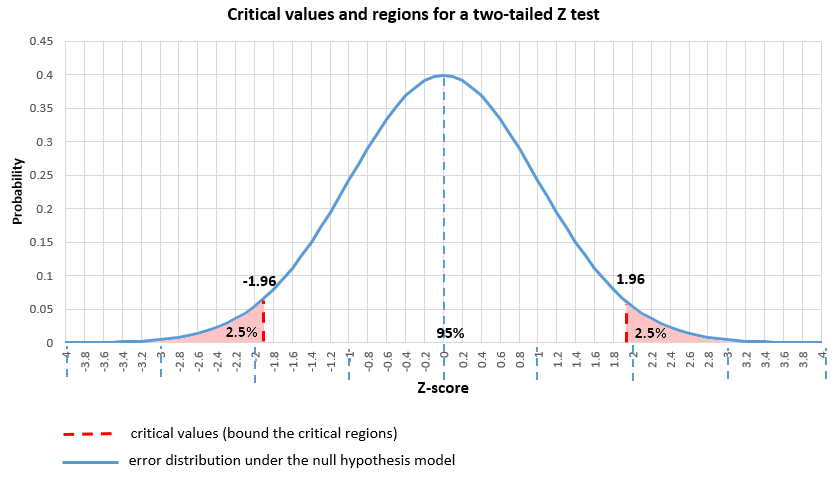
The distance function would vary depending on the distribution of the error: Z, T, F, or Chi-square (X2). The calculation of a particular critical value based on a supplied probability and error distribution is simply a matter of calculating the inverse cumulative probability density function (inverse CPDF) of the respective distribution. This can be a difficult task, most notably for the T distribution [2].
T critical value calculation
The T-distribution is often preferred in the social sciences, psychiatry, economics, and other sciences where low sample sizes are a common occurrence. Certain clinical studies also fall under this umbrella. This stems from the fact that for sample sizes over 30 it is practically equivalent to the normal distribution which is easier to work with. It was proposed by William Gosset, a.k.a. Student, in 1908 [3], which is why it is also referred to as "Student's T distribution".
To find the critical t value, one needs to compute the inverse cumulative PDF of the T distribution. To do that, the significance level and the degrees of freedom need to be known. The degrees of freedom represent the number of values in the final calculation of a statistic that are free to vary whilst the statistic remains fixed at a certain value.
It should be noted that there is not, in fact, a single T-distribution, but there are infinitely many T-distributions, each with a different level of degrees of freedom. Below are some key values of the T-distribution with 1 degree of freedom, assuming a one-tailed T test is to be performed. These are often used as critical values to define rejection regions in hypothesis testing.
| Probability value | Degrees of Freedom | T critical value |
|---|---|---|
| 0.2000 | 1 | 1.3764 |
| 0.1000 | 1 | 3.0777 |
| 0.0500 | 1 | 6.3138 |
| 0.0250 | 1 | 12.7062 |
| 0.0200 | 1 | 15.8946 |
| 0.0100 | 1 | 31.8205 |
| 0.0010 | 1 | 318.3088 |
| 0.0005 | 1 | 636.6193 |
Z critical value calculation
The Z-score is a statistic showing how many standard deviations away from the normal, usually the mean, a given observation is. It is often called just a standard score, z-value, normal score, and standardized variable. A Z critical value is just a particular cutoff in the error distribution of a normally-distributed statistic.
Z critical values are computed by using the inverse cumulative probability density function of the standard normal distribution with a mean (μ) of zero and standard deviation (σ) of one. Below are some commonly encountered probability values (significance levels) and their corresponding Z values for the critical region, assuming a one-tailed hypothesis.
| Probability value | Z critical value |
|---|---|
| 0.2000 | 0.8416 |
| 0.1000 | 1.2816 |
| 0.0500 | 1.6449 |
| 0.0250 | 1.9600 |
| 0.0200 | 2.0537 |
| 0.0100 | 2.3263 |
| 0.0010 | 3.0902 |
| 0.0005 | 3.2905 |
The critical region defined by each of these would span from the Z value to plus infinity for the right-tailed case, and from minus infinity to minus the Z critical value in the left-tailed case. Our calculator for critical value will both find the critical z value(s) and output the corresponding critical regions for you.
Chi Square (Χ2) critical value calculation
Chi square distributed errors are commonly encountered in goodness-of-fit tests and homogeneity tests, but also in tests for independence in contingency tables. Since the distribution is based on the squares of scores, it only contains positive values. Calculating the inverse cumulative PDF of the distribution is required in order to convert a desired probability (significance) to a chi square critical value.
Just like the T and F distributions, there is a different chi square distribution corresponding to different degrees of freedom. Hence, to calculate a Χ2 critical value one needs to supply the degrees of freedom for the statistic of interest.
F critical value calculation
F distributed errors are commonly encountered in analysis of variance (ANOVA), which is very common in the social sciences. The distribution, also referred to as the Fisher-Snedecor distribution, only contains positive values, similar to the Χ2 one. Similar to the T distribution, there is no single F-distribution to speak of. A different F distribution is defined for each pair of degrees of freedom - one for the numerator and one for the denominator.
Calculating the inverse cumulative PDF of the F distribution specified by the two degrees of freedom is required in order to convert a desired probability (significance) to a critical value. There is no simple solution to find a critical value of f and while there are tables, using a calculator is the preferred approach nowadays.
References
1 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science. The Netherlands: Elsevier.
2 Shaw T.W. (2006) – "Sampling Student's T distribution – use of the inverse cumulative distribution function", Journal of Computational Finance 9(4):37-73, DOI:10.21314/JCF.2006.150
3 "Student" [William Sealy Gosset] (1908) - "The probable error of a mean", Biometrika 6(1):1–25. DOI:10.1093/biomet/6.1.1
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Critical Value Calculator", [online] Available at: https://www.gigacalculator.com/calculators/critical-value-calculator.php URL [Accessed Date: 02 Jan, 2026].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:












 Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".
Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".