Correlation Coefficient Calculator
Use this correlation calculator to estimate the correlation coefficient of any two sets of data. The tool can compute the Pearson correlation coefficient r, the Spearman rank correlation coefficient (rs), the Kendall rank correlation coefficient (τ), and the Pearson's weighted r for any two random variables. It also computes p-values, z scores, and confidence intervals, as well as the least-squares regression equation.
- What is a correlation coefficient
- Using the correlation coefficient calculator
- Pearson's vs. Spearman's vs Kendall's coefficient
- Correlation coefficient equations
- Pearson's correlation coefficient formula
- Spearman rank correlation formula
- Kendall's tau formula
- Weighted correlation coefficient
- Practical applications of correlation
What is a correlation coefficient
The phenomenon measured by a correlation coefficient is that of statistical correlation. We say two random variables or bivariate data are correlated if there is some form of quantifiable association between them, some kind of statistical relationship. A trivial example would be to plot the change in average daily temperature and the consumption of ice cream, or the intensity of cloud coverage and rainfall precipitation in a given region. We will observe that the two variables tend to change together, to an extent, suggesting some dependence between them. The dependence might be due to direct causality, indirect causality, or it might be entirely spurious.
A correlation coefficient calculated for two variables, X and Y, is a measure of the extent to which the dependent variable (Y) tends to change with changes in the independent variable (X). It quantifies both the strength and the direction of the relationship. A positive correlation coefficient reflects a straight relationship between the variables while a negative one reflects an inverse one (when X is higher, Y is lower, and vice versa). A coefficient of zero signifies complete lack of a statistical association (orthogonality), while a coefficient of one (or minus one) suggests a perfect correlation (X and Y change in unison).
We can therefore distinguish between three basic types of correlation:
- No correlation - the coefficient is exactly 0.
- Positive correlation - the coefficient is between 0 and 1
- Negative correlation - the coefficient is between -1 and 0
An example of a negative correlation is shown below, with the accompanying Pearson's correlation coefficient (R).
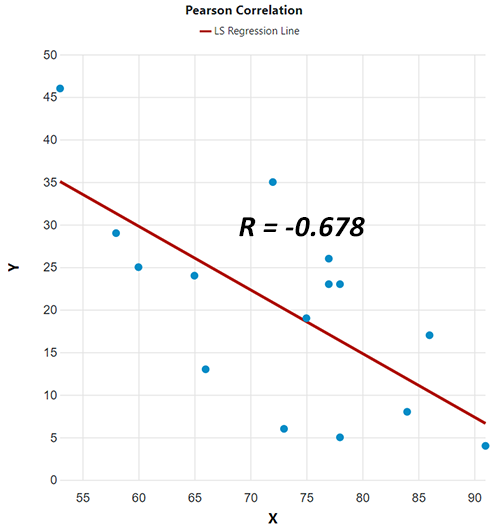
There are different types of coefficients quantifying different types of correlations in terms of how the variables relate to each other - linear / non-linear, functional / non-functional, etc. (see Pearson's vs. Spearman's vs Kendall's coefficient below). As any other statistic, a coefficient of correlation is just an estimate and has inherent uncertainty. A Z score, p-value, and confidence intervals can be used to quantify the uncertainty of any correlation coefficient. Our correlation coefficient calculator supports the three most popular coefficients and uncertainty estimates for all of them.
Using the correlation coefficient calculator
To use this correlation coefficient calculator first enter the data you want to analyze: one column per variable, X and Y. Optionally, you can enter pair weights in a third column, in which case they will be applied to the values resulting in a weighted correlation coefficient (only applies to Pearson's coefficient). Columns are separated by spaces, tabs, or commas, so copy-pasting from Excel or another spreadsheet should work just fine. All columns should have an equal number of values in them.
Then you need to select the type of coefficient to compute. Coefficients supported in the calculator are:
- Pearson correlation coefficient (r)
- Spearman correlation coefficient (rs)
- Kendall correlation coefficient (τ)
The appropriate coefficient will depend on the type of your data and the type of correspondence that is thought to underlie the supposed dependence. This step is crucial in drawing correct conclusions about the presence or absence of correlation, as well as its strength. If you need guidance on this, the comparison of the three coefficients of correlation that this calculator supports can be found below and should be of great assistance.
Finally, you can change the default 95% confidence level for the computed confidence intervals. The p-values and confidence intervals for the Pearson coefficient and the Spearman coefficient are calculated using the Fisher transformation and hold under an independence of observations assumption. The same assumption applies to estimates related to the Kendall rank correlation coefficient.
The coefficient of correlation calculator will produce as output the selected coefficient and the sample size. It will also output the z score, p-value, and confidence intervals (two-sided bounds and one-sided bounds) for all but the weighted Pearson's coefficient. The output also includes the least-squares regression equation (regression line) of the form y = m · x + b where m is the slope and b is the y-intercept of the regression line.
Pearson's vs. Spearman's vs Kendall's coefficient
The choice of the correct correlation coefficient is essential in making correct inferences. Violating the assumptions behind a statistical model results in meaningless (or misleading) numbers. Choosing the wrong coefficient can also mean that you will fail to capture a true correlation, e.g. if you use Pearon's coefficient while the relationship is non-linear. As Arndt et al. put it: "The wrong choice can obscure significant findings due to low power or lead to spurious associations because of an inflated type I error rate." [5].
To help you with this choice when using this calculator, below is a table with essential characteristics and assumptions for the three most used coefficients, as well as guidance on when to use which.
| Attribute / Test | Pearson's r | Spearman's r | Kendall's tau |
|---|---|---|---|
| Supported data types | Interval, Ratio | Ordinal, Interval, Ratio | Ordinal, Interval, Ratio |
| Homogeneity assumptions | Homoscedasticity | None | None |
| Dependence assumptions | Linear dependence | Monotonic dependence | Monotonic dependence |
| Susceptibility to outliers (robustness) | Sensitive | Robust | Robust |
| Inference assumptions (H0 for p-values, CI coverage) |
The sample pairs are independent and identically distributed (IID) and follow a bivariate normal distribution | The sample pairs are independent and identically distributed (IID) | The sample pairs are independent and identically distributed (IID) |
| Inference if coefficient is 0: | X and Y are linearly uncorrelated random variables* | X and Y are monotonically uncorrelated random variables* | X and Y are monotonically uncorrelated random variables* |
| Inference if coefficient is 1 or -1 | X and Y are perfectly linearly dependent random variables | X and Y are perfectly monotonically dependent random variables | X and Y are perfectly monotonically dependent random variables |
* Note that lack of correlation does not necessitate independence whereas the presence of correlation signifies dependence.
Since it is often mistakenly believed that Pearson's r requires that both X and Y are normally distributed, it warrants repeating that this is not so. As noted by Spearman [2] "...the method of "product moments" is valid, whether or not the distribution follows the normal law of frequency, so long as the 'regression' is linear". So neither coefficient relies on distributional assumptions for its validity.
Normality is an assumption only for the calculation of related statistics and if those are of interest you can use our normality test calculator to check for departures. Keep in mind that high p-values from the normality tests might be just due to having a small sample size and tests not being sensitive enough.
As you can see, making the right choice is not a trivial matter as it requires knowing your data and understanding the potential dependence. Make sure you understand the implications of selecting one correlation method over the other.
Correlation coefficient equations
The correlation coefficient calculator supports several different coefficients. The equations used to compute each of them are explained here in some detail.
Pearson's correlation coefficient formula
The formula for computing Pearson's ρ (population product-moment correlation coefficient, rho) is as follows [1]:
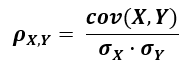
where cov(X,Y) is the covariance of the variables X and Y and σX (sigma X) is the population standard deviation of X, and σY of Y. Mathematically, it is defined as the quality of least squares fitting to the original data. It is applicable when we know the population mean and standard deviations, which is rarely the case in practice. Hence most of the time the applicable formula is the equation for the Pearson sample correlation coefficient r.
The formula for Pearson's r is [1]:
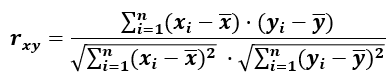
which is essentially the same as for Pearson's ρ, but instead of population means and standard deviations we have sample means and standard deviations. The numerator represents the sample covariance cov(x,y) while the denominator is the product of the sample standard deviations σx and σy. The large Σ operator is the familiar summation operator. This equation makes it easy to see why correlation can be defined as a standardized form of the covariance.
Spearman rank correlation formula
The formula for computing Spearman's rs (Spearman's rank correlation coefficient) is as follows [2]:
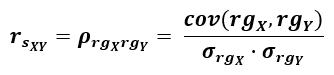
where rgX and rgY stand for the rank transformed values of X and Y. Therefore, Spearman's correlation coefficient rs is simply the Pearson correlation coefficient computed using the rank values instead of the raw values of the two variables, which is why it can uncover non-linear, as well as linear relationships between X and Y, as long as Y is a monotone function of X. In other words, the Spearman rs assesses how well an arbitrary monotonic function can describe a relationship between two variables, without imposing any assumptions on the frequency distribution of the variables [4].
Kendall's tau formula
The formula for computing the Kendall rank correlation coefficient τ (tau), often referred to as Kendall's τ coefficient or just Kendall's τ, is as follows [3]:
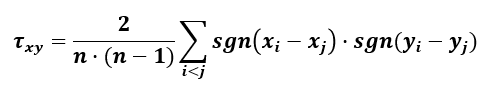
Where n is the number of pairs and sgn() is the standard sign function. The coefficient computed with the above equation is known as (τA) and only works when there are no ties in the data. The calculator uses a slightly modified equation (τB) which accounts correctly for ties within the datasets [6].
Kendall's tau quantifies the similarity of the orderings of ranked transformed data and can be interpreted as the probability that as X increases Y will increase rescaled from -1 to 1. This coefficient was not as popular in the near past mainly due to its prohibitive computational complexity, but the ease of interpretation and its other desirable qualities - high power with good robustness, coupled with an intuitive interpretation as the probability that any pair of observations will have the same ordering on both variables rescaled from -1 to 1 [5] - make it a prime candidate for many research questions.
Weighted correlation coefficient
The formula for computing the weighted Pearson correlation coefficient is as follows:
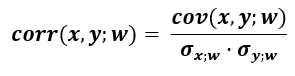
The equation consists of the weighted covariance of x and y divided by the product of the weighted standard deviations of x and y. The weighted covariance of x and y given a vector of weights w can be computed as:
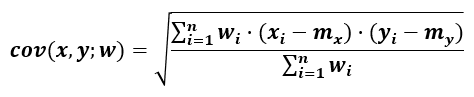
where mx and my are the weighted means of x and y computed in the usual manner.
Using the same notation, the formula for the weighted standard deviation is:
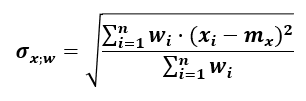
It is computed equivalently for y.
Practical applications of correlation
Correlation and correlation coefficients have broad applications in multiple scientific and applied disciplines like biology, genetics, epidemiology, psychology (psychometrics), psychiatry, finance, stock trading, marketing, management, and countless others. In a simple linear regression fitted by least-squares the coefficient of determination is simply Pearson's r squared (r2).
A prominent case we can examine as a practice problem is the association of smoking with various diseases and shortened lifespan. When observing population wide health trends, researchers noticed a potential link between smoking and various diseases, many cancers included, as well as all-cause mortality. What does one such correlation look like? Let's say we take a representative sample from men 50 years and older who smoke, and measure both the number of cigarettes they consume per day and the age at which they died. The number of cigarettes is our independent variable X, whereas longevity in years is our dependent variable Y.
| Metric / Case |
|---|
| Cigarettes/day |
| Longevity |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 46 | 17 | 26 | 5 | 23 | 24 | 35 | 29 | 4 | 13 | 8 | 6 | 23 | 19 |
| 60 | 53 | 86 | 77 | 78 | 77 | 65 | 72 | 58 | 91 | 66 | 84 | 73 | 78 | 75 |
Putting the numbers in the calculator and selecting to use Kendall's correlation coefficient we can quantify the relationship between smoking and longevity. In this case the coefficient is -0.541 meaning that there exists a moderate inverse association between X and Y. The higher the number of cigarettes, the lower the longevity - a dose-dependent relationship. The resulting p-value of 0.0022 shows that observing such a negative correlation would be highly unlikely if there were none or positive correlation instead.
References
1 Pearson K. (1896) "Mathematical contributions to the theory of evolution. III. Regression, heredity, and panmixia", Philosophical Transactions A 373:253–318
2 Spearman C. (1904) "The proof and measurement of association between two things", American Journal of Psychology 15(1):72–101; DOI:10.2307/1412159
3 Kendall M. (1938) "A New Measure of Rank Correlation", Biometrika 30(1–2):81–89; DOI:10.1093/biomet/30.1-2.81
4 Hauke J., Kossowski T. (2011) "Comparison of Values of Pearson's and Spearman's Correlation Coefficients on the Same Sets of Data", Quaestiones Geographicae 30(2):87-93; DOI: 10.2478/v10117-011-0021-1
5 Arndt et al (1999) "Correlating and Predicting Psychiatric Symptom Ratings - Spearman's r Versus Kendall's Tau Correlation", Journal of Psychiatric Research, 33(2):97-104; DOI: 10.1016/s0022-3956(98)90046-2
6 Knight W. (1966) "A Computer Method for Calculating Kendall's Tau with Ungrouped Data", Journal of the American Statistical Association 61(314):436–439; DOI:10.2307/2282833
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Correlation Coefficient Calculator", [online] Available at: https://www.gigacalculator.com/calculators/correlation-coefficient-calculator.php URL [Accessed Date: 31 Dec, 2025].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:












 Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".
Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".