Odds Ratio Calculator
Use this odds ratio calculator to easily calculate the ratio of odds, confidence intervals and p-values for the odds ratio (OR) between an exposed and control group. One and two-sided confidence intervals are reported, as well as Z-scores.
- Using the odds ratio calculator
- What are odds and what is an odds ratio?
- Odds ratio vs. Risk Ratio (Relative Risk)
- Standard error and confidence interval formula for odds ratios
- What is an odds ratio confidence interval and "confidence level"
- One-sided vs. two-sided intervals
Using the odds ratio calculator
This odds ratio calculator allows you to perform a post-hoc statistical evaluation of odds data when the outcome of interest is the change in the odds (the odds ratio) between an exposed/treatment group and a control group. To use the tool you need to simply enter the number of events and non-events (e.g. disease and no disease) for each of the two groups. You can select any level of significance you require for the confidence intervals.
The odds ratio calculator will output: odds ratio, two-sided confidence interval, left-sided and right-sided confidence interval, one-sided p-value and z-score. If the test was two-sided, you need to multiply the p-value by 2 to get the two-sided p-value.
What are odds and what is an odds ratio?
Odds are the probability of an event occurring (e.g. developing a disease or condition, being injured, dying, etc.) versus the event not occurring (e.g. staying disease-free, symptom-free, staying alive, etc.), usually between an exposed group and a control group, or a treatment group and a control group, depending on context (though connected, betting odds are a different breed). An odds ratio (OR) expresses the ratio of two odds: OR = (Eventstreatment / Non-eventstreatment) / (Eventscontrol / Non-eventscontrol). If the odds ratio equals 1 there is no effect of the treatment or exposure.
Here is a practical example. Take smokers and risk of lung cancer and assume in a given sample in the exposed group (smokers) 20 developed some kind of lung cancer and 80 remained cancer free, while in the non-smokers 1 person developed lung cancer and 99 remained cancer-free, what are the relative odds of smokers versus non-smokers?
Denoting smokers who developed cancer with a, those who did not with b, then non-smokers who developed cancer with c and those who did not with d the formula and solution to calculate the odds ratio looks as such:
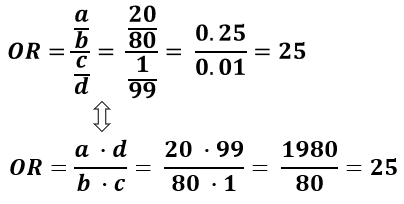
This is the equation used in our odds ratio calculator. So a smoker will have 25 higher odds to develop lung cancer compared to a non-smoker. The odds ratio should not be confused with relative risk or hazard ratios which might be close in certain cases, but are completely different measures.
Odds ratio vs. Risk Ratio (Relative Risk)
Odds ratios are not very intuitive to understand, but are sometimes used due to convenience in plugging them in other statistics. Where possible the relative risk (risk ratio) should be reported instead due to it being much more intuitive measure of effectiveness. Still, odds ratios are widely used in fields like epidemiology, clinical research, including randomized control trials, as well as cohort analysis and longitudinal observational studies.
One possible advantage of odds ratios is that they are invariant to the variable of interest. Odds ratios calculated using our tool will vary proportionally in both effect directions while a risk ratio is skewed and can produce very different results when looking at the complimentary proportion instead. As an extreme example of the difference between risk ratio and odds ratio, if action A carries a risk of a negative outcome of 99.9% while action B has a risk of 99.0% the relative risk is approximately 1 while the odds ratio between A and B is 10 (1% = 0.1% x 10), more than 10 times higher.
The highly disparate results in RR vs OR are due to the definition of risk based on the negative events. If risk is defined by using the positive outcome instead, the value of relative risk is 0.10 which has a much better correspondence with the odds ratio. However, assuming the variable of interest is properly defined this counts as a disadvantage for odds ratios which is why risk ratios are generally preferred. When discussing risk reduction the relative risk defined via the risk event (odds ratio can easily be misinterpreted) should be used, but if one is interested in the increase in non-events in the above example then the reverse relative risk should be reported (the odds ratio now corresponds closely to the relative risk).
Standard error and confidence interval formula for odds ratios
The standard error of the log risk ratio is known to be:

Accordingly, confidence intervals are calculated using the formula:

where OR is the calculated odds ratio (relative odds), SElnOR is the standard error for the log odds ratio and Z is the score statistic, corresponding to the desired confidence level. For reference, this is the formula used for CI limit calculations in this odds ratio calculator. The Z-score corresponding to a two-sided interval at level α (e.g. 0.90) is calculated for Z1-α/2, revealing that a two-sided interval, similarly to a two-sided p-value, is calculated by conjoining two one-sided intervals with half the error rate. E.g. a Z-score of 1.6448 is used for a 0.95 (95%) one-sided confidence interval and a 90% two-sided interval, while 1.956 is used for a 0.975 (97.5%) one-sided confidence interval and a 0.95 (95%) two-sided interval. Therefore it is important to use the right kind of interval: more on one-tailed vs. two-tailed intervals.
What is an odds ratio confidence interval and "confidence level"
A confidence interval is defined by an upper and lower limit for the value of a variable of interest and it aims to aid in assessing the uncertainty associated with a measurement, usually in an experimental context. The wider an interval is, the more uncertainty there is in the odds ratio estimate.
Every confidence interval is constructed based on a particular required confidence level, e.g. 0.09, 0.95, 0.99 (90%, 95%, 99%) which is also the coverage probability of the interval. A 95% confidence interval (CI), for example, will contain the true value of interest 95% of the time (in 95 out of 5 similar experiments).
Simple two-sided confidence intervals are symmetrical around the observed odds ratio, but in certain scenarios asymmetrical intervals may be produced (complex cases, not supported by our calculator). In any particular case the true odds ratio may lie anywhere within the interval, or it might not be contained within it, no matter how high the confidence level is. Raising the confidence level widens the interval, while decreasing it makes it narrower, as you can verify simply by setting a different level in our odds ratio calculator. Similarly, larger sample sizes result in narrower intervals, since the interval's asymptotic behavior is to be reduced to a single point.
One-sided vs. two-sided intervals
While odds ratio confidence intervals are customarily given in their two-sided form, this can often be misleading if one is interested if a particular value below or above the interval can be excluded at a given significance level. A one-sided interval in which one side is plus or minus infinity is appropriate when we have a null / want to make statements about an odds ratio value lying either above or below the top / bottom bound [1]. By design a two-sided interval is constructed as the overlap between two one-sided intervals at 1/2 the error rate 2.
For example, if a two-sided 90% odds ratio interval covers (2.5, 10), one can say that odds ratios less than 2.5 are excluded with 95% confidence precisely because a 90% two-sided interval is nothing more than two conjoined 95% one-sided intervals:
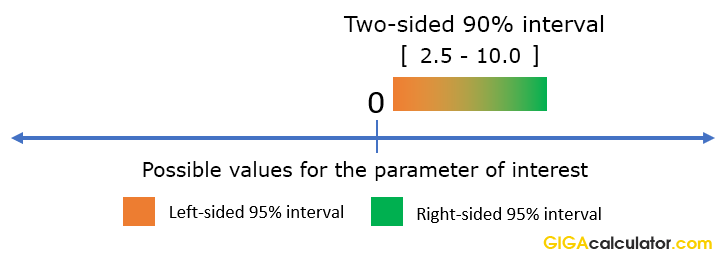
Therefore, to make directional statements about relative odds based on two-sided intervals, one needs to increase the significance level for the statement. In such cases it is better to use the appropriate one-sided odds ratio interval instead, to avoid confusion. Our free odds ratio calculator conveniently produces both one-sided intervals for you.
References
1 Georgiev G.Z. (2017) "One-tailed vs Two-tailed Tests of Significance in A/B Testing", [online] https://blog.analytics-toolkit.com/2017/one-tailed-two-tailed-tests-significance-ab-testing/ (accessed Apr 28, 2018)
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Odds Ratio Calculator", [online] Available at: https://www.gigacalculator.com/calculators/odds-ratio-calculator.php URL [Accessed Date: 06 Jan, 2026].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:












 Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".
Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".