Error Function Calculator
Use this ERF calculator to easily calculate the Gauss error function erf(x) for any real-valued x and the inverse error function erf-1(y), y ∈ [-1, 1]. It can also output their complementary functions erfc(x) and erfc-1(y). High-precision calculation up to 25 significant digits. A table of x values and corresponding values of erf and erfc is included as reference.
- Using the error function calculator
- What is an error function?
- Error function formula
- Inverse error function
- Error function table
- Example application
Using the error function calculator
The erf calculator can be used to compute the error function of any number on the real line. The output also contains the complementary error function for the same number as well as a function plot showing where erf(x) lies relative to other possible function values. erf(x) returns a result between zero and one for any real value of x.
In inverse error function mode the output contains the inverse of erf and its complement. The input y needs to be a real number between minus one and one (y ∈ [-1, 1]).
What is an error function?
In mathematics and statistics, the error function a.k.a. the Gauss error function or just erf, is a complex function of a complex variable defined as [1,2]:
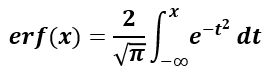
Aside from applied mathematics where it is used to solve differential equations and in physics in solutions of the heat equation in the case where boundary conditions are given by the Heaviside step function, it also sees use in statistics where the inverse error function is used in the calculation of critical values, p-values, confidence intervals which are all related to statistical hypothesis testing and estimation.
The function plot illustrates its sigmoid shape:

Since e-t2 is an even function and erf(-x) = -erf(x), the error function is an odd function.
Error function formula
To calculate erf(x) one performs an integration from minus infinity to x of the equation e-t2. The formula can therefore be expressed by the following integral equation:
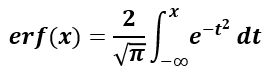
The equation has no closed-form solution and various approximations are in use. In this calculator we use a polynomial approximation with a maximal error of 1.2 × 107 for any real argument as per reference [3].
Complementary error function
The equation for the complementary error function is given by:
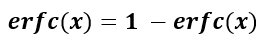
Its solution is a simple subtraction from one. It sees application in physics problems.
Inverse error function
The inverse error function, denoted erf-1(y) takes as input the result of y = erf(x), and produces the corresponding x value. While a true inverse function would be multivalued and thus would not have a unique solution, for values of y between −1 and 1 there is a unique real number solution to the equation:

The solution can easily be found by various root-finding methods.
Error function table
An erf table contains tabulated values of real numbers and their corresponding error function values.
Table of commonly used numbers:
| x | erf(x) | erfc(x) |
|---|---|---|
| 0.000 | 0.000000 | 1.000000 |
| 0.01 | 0.011283 | 0.988717 |
| 0.02 | 0.022565 | 0.977435 |
| 0.05 | 0.056372 | 0.943628 |
| 0.10 | 0.112463 | 0.887537 |
| 0.20 | 0.222703 | 0.777297 |
| 0.30 | 0.328627 | 0.671373 |
| 0.40 | 0.428392 | 0.571608 |
| 0.50 | 0.520500 | 0.479500 |
| 0.60 | 0.603856 | 0.396144 |
| 0.70 | 0.677801 | 0.322199 |
| 0.80 | 0.742101 | 0.257899 |
| 0.90 | 0.796908 | 0.203092 |
| 1.00 | 0.842701 | 0.157299 |
| 1.10 | 0.880205 | 0.119795 |
| 1.20 | 0.910314 | 0.089686 |
| 1.30 | 0.934008 | 0.065992 |
| 1.40 | 0.952285 | 0.047715 |
| 1.50 | 0.966105 | 0.033895 |
| 1.60 | 0.976348 | 0.023652 |
| 1.70 | 0.983790 | 0.016210 |
| 1.80 | 0.989091 | 0.010909 |
| 1.90 | 0.992790 | 0.007210 |
| 2.00 | 0.995322 | 0.004678 |
| 2.25 | 0.998537 | 0.001463 |
| 2.50 | 0.999593 | 0.000407 |
| 2.75 | 0.999899 | 0.000101 | 3.00 | 0.999978 | 0.000022 | 3.50 | 0.999999 | 0.000001 | 4.00 | 1.000000 | 0.000000 |
Example application
The inverse error function can be used to compute the quantile function (inverse distribution function) of a normal distribution. For example, if we want to find the cut-off for the top decile of a normal distribution with mean μ = 0 and standard deviation σ = 3, we would use the equation:
F-1(0.9) = μ + σ · √2 · erf-1(2 · p - 1)
Knowing that the top decile represents the top 10 percent, we need to find the cut-off at 90%, or 0.9. Replacing the known values we get:
F-1(0.9) = 0 + 3 · √2 · erf-1(2 · 0.9 - 1) = 3 · √2 · erf-1(0.8)
Using a square root calculator we find √2 equals 1.4142 and using this calculator we find erf-1(0.8) = 0.9062. Replacing once again we find the solution:
F-1(0.9) = 3 · 1.4142 · 0.9062 = 3.8446 which is accurate to four significant digits, same as the accuracy of all numbers used in obtaining the result.
References
1 Glaisher, J.W.L. (1871) "On a class of definite integrals" London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 4 42(277): 294–302. DOI 10.1080/14786447108640568
2 Glaisher, J.W.L. (1871) "On a class of definite integrals. Part II." London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 4 42(279): 421–426. DOI 10.1080/14786447108640600
3 "Numerical Recipes in Fortran 77: The Art of Scientific Computing" (1992), page 214, Cambridge University Press ISBN 0-521-43064-X
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation:
Georgiev G.Z., "Error Function Calculator", [online] Available at: https://www.gigacalculator.com/calculators/error-function-calculator.php URL [Accessed Date: 09 Jan, 2026].
 Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".
Georgi Georgiev is an applied statistician with background in statistical analysis of online controlled experiments, including developing statistical software, writing over one hundred articles and papers, as well as the popular book "Statistical Methods in Online A/B Testing".